Перейти к контенту
Решение неравенств методом интервалов
Для решения неравенств методом интервалов применяем следующие теоремы:
1. Если функция f непрерывна на некотором промежутке и не имеет на нём нулей, то она на этом промежутке сохраняет постоянный знак.
2. Функция y = 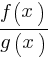 , где f(x) и g(x) – многочлены, непрерывна на D(y).
, где f(x) и g(x) – многочлены, непрерывна на D(y).
Рассмотрим несколько примеров
Пример 1: Решите неравенство (x + 4)(x + 2)(x – 5) > 0.
Нулями функции f(x) являются числа -4, -2, 5. Эти числа разбивают множество R на промежутки знакопостоянства.
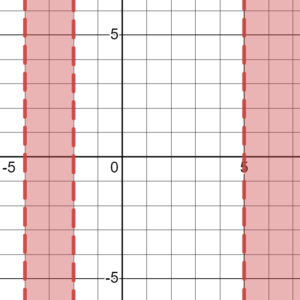
Методом подстановки пробных точек, определим, что знак “+” находится на промежутке (-4; -2) и на промежутке (5; +∞). Ответ x ∈ (-4; -2) ⋃ (5; +∞).
Пример 2: Решите неравенство 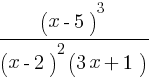 < 0.
< 0.
Нулями данного неравенства будут являться -1/3, 2, 5.
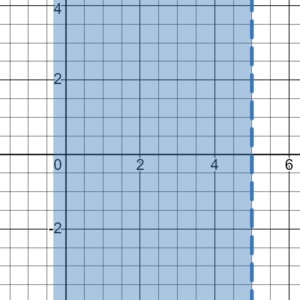
Методом подстановки пробных точек, определим, что знак “-” находится на промежутке (-1/3; 2) и на промежутке (2; 5). Ответ x ∈ (-1/3; 2) ⋃ (2; 5).
Пример 3: Решите неравенство 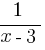 >
> 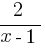 .
.
Для начала снесём всё в левую часть: 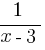 –
– 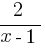 > 0. Приведём левую часть к общему знаменателю:
> 0. Приведём левую часть к общему знаменателю: 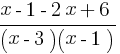 > 0. Получим
> 0. Получим 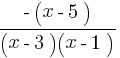 > 0. Нулями будут являться числа 1, 3, 5.
> 0. Нулями будут являться числа 1, 3, 5.
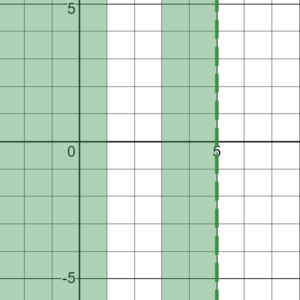
Методом подстановки пробных точек, определим, что знак “+” находится на промежутке (–∞; 1) и на промежутке (3; 5). Ответ x ∈ (-∞; 1) ⋃ (3; 5).
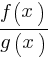 , где f(x) и g(x) – многочлены, непрерывна на D(y).
, где f(x) и g(x) – многочлены, непрерывна на D(y).
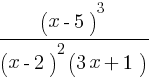 < 0.
< 0.
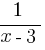 >
> 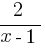 .
.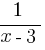 –
– 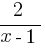 > 0. Приведём левую часть к общему знаменателю:
> 0. Приведём левую часть к общему знаменателю: 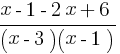 > 0. Получим
> 0. Получим 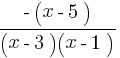 > 0. Нулями будут являться числа 1, 3, 5.
> 0. Нулями будут являться числа 1, 3, 5.