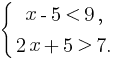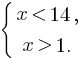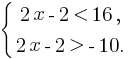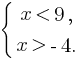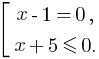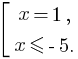6. Системы и совокупности линейных неравенств с одной переменной – На 5 !!!

Системы и совокупности линейных неравенств с одной переменной

Решение системы неравенств с одной переменной – значение переменной, которое образует каждое неравенство системы в верное числовое неравенство.

Чтобы решить систему неравенств, необходимо найти множество её решений.

Для решения системы неравенств надо найти пересечение множеств решений неравенств, входящих в систему.

Решить совокупность неравенств – найти объединение множеств решений неравенств.

Рассмотрим несколько примеров

Пример 1: Решить систему неравенств:

delim{lbrace}{matrix{2}{1}{{x-5 lt 9,} {2x+5 gt 7.}}}{}

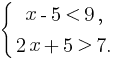
Преобразуем каждое неравенство этой системы в равносильное ему:

delim{lbrace}{matrix{2}{1}{{x lt 14,} {x gt 1.}}}{}

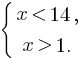
Решением этой системы будет являться интервал (1; 14).

Пример 2: Решите неравенство -10 < 2x – 2 < 16.

Представим данное неравенство в виде системы:

delim{lbrace}{matrix{2}{1}{{2x-2 lt 16,} {2x-2 gt -10.}}}{}

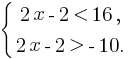
Преобразуем каждое неравенство этой системы в равносильное ему:

delim{lbrace}{matrix{2}{1}{{x lt 9,} {x gt -4.}}}{}

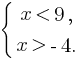
Решением этой системы будет являться интервал (-4; 9).

Пример 3: Решите неравенство (x – 1)²(x + 5) ≤ 0.

Это неравенство равносильно совокупности:

delim{[}{matrix{2}{1}{{x-1=0,}{x+5 le 0.}}}{}

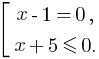
Преобразуем каждое неравенство этой совокупности в равносильное ему:

delim{[}{matrix{2}{1}{{x=1,}{x le -5.}}}{}

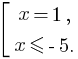
Решением данной совокупности будет промежуток (-∞; -5] ⋃ {1}.