7. Неравенства и уравнения, содержащие знак модуля 

Неравенства и уравнения, содержащие знак модуля 

 Модуль числа x – расстояние от точки, изображающей число x на координатной прямой, до начала отсчёта. 

Модуль числа x обозначается |x|.

По определению модуля:

|x| = x, если x ≥ 0 и -x, если x < 0.

Чтобы раскрыть модуль, необходимо знать знак числа.

 Например: 

|x – 5| = 5 – x, если x < 5.

 Рассмотрим свойства модуля: 

1) Модуль любого числа принимает только неотрицательные значения (|x|≥ 0).

2) Модули противоположных чисел равны (|x|=|-x|).

3) Если |x|= y, то y ≥ 0 и x = y или x = -y.

4) Если y ≥ 0 и x = y или x = -y, то |x| = y.

5) Расстояние между точками X(x) и Y(y) на координатной прямой равно |x – y|.

 Рассмотрим некоторые теоремы для решения уравнений с модулем: 

1. Если x ≥ 0, то уравнение вида |y| = x равносильно совокупности

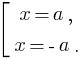
2. Уравнение вида |f(x)|=g(x) равносильно системе:

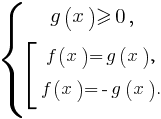
3. Неравенство вида |x|< y равносильно системе:

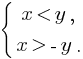
4. Неравенство вида |f(x)|< g(x) равносильно системе неравенств:

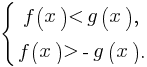
5. Неравенство вида |x|> y равносильно совокупности неравенств:

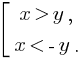
5. Неравенство вида |f(x)|> g(x) равносильно совокупности неравенств:

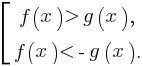
 Рассмотрим несколько примеров  

 Пример 1:  Решите уравнение |x – 5| = 7.

Убрав модуль, получим совокупность уравнений:

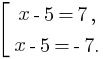
Получим x = 12, x = -2.

 Пример 2:  Решите уравнение |x + 3| = 4x – 9.

Уравнение равносильно системе:

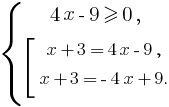
Упростив систему, получим x > 2,25 и x = 4 и x = 1,2. Ответом будет являться x = 4.

 Пример 3:  Решите неравенство |4x – 2| < 3.

Преобразуем выражение в систему, получим:

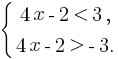
Отсюда:

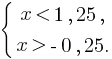
Ответом будет являться интервал (-0,25; 1,25).

 Пример 4:  Решите неравенство |3x – 1| > 2.

Неравенство равносильно совокупности неравенств:

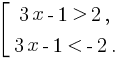
Получим совокупность:

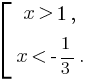
Ответом будет являться (-∞; 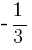) ⋃ (1; +∞).
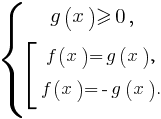
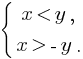
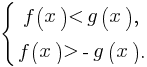
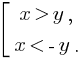
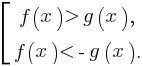
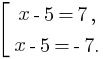
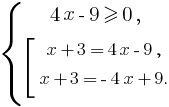
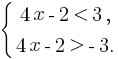
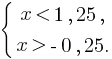
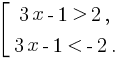
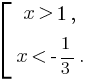
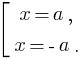
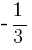