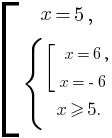2. Квадратный корень и арифметический квадратный корень

Квадратный корень и арифметический квадратный корень

Квадратный корень из числа x – число, квадрат которого равен x.

Например: квадратными корнями из числа 25 являются числа -5 и 5.

Арифметический квадратный корень из числа x – неотрицательное число, квадрат которого равен x.

Например, арифметический квадратный корень из 100 – число 10.

Арифметический квадратный корень обозначают так: √(знак квадратного корня или радикал).

Подкоренное выражение – выражение, стоящее под знаком радикала. Например: .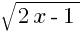

Действие нахождения арифметического квадратного корня из числа – извлечение квадратного корня.

Также для любого неотрицательного числа x справедливо: 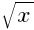≥ 0 и (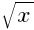)² = x.

Если x ≥ 0, то уравнение вида y² = x равносильно совокупности:

delim{[}{matrix{2}{1}{{y=sqrt{x},}{y=-sqrt{x}.}}}{}

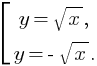
Рассмотрим несколько примеров

Пример 1: Найдите значение выражения (-4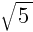)².

Попробуйте решить эту задачу самостоятельно, а если не получается, то просто нажмите на это предложение.

Пример 2: Решите уравнение (2x – 3)² = 5.

Уравнение равносильно совокупность двух уравнений:

delim{[}{matrix{2}{1}{{2x-3=sqrt{5},}{2x-3=-sqrt{5}.}}}{}

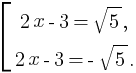
Получим совокупность:

delim{[}{matrix{2}{1}{{x={sqrt{5}+3}/{2},}{x={3-sqrt{5}}/{2}.}}}{}

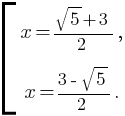
Пример 3: Решите уравнение (x² – 36)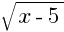 = 0.

Найдём область определения этого уравнения: x – 5 ≥ 0, значит x ≥ 5. Получим совокупность:

$delim{[}{matrix{3}{1}{{sqrt{x-5}=0,}{delim{lbrace}{matrix{3}{1}{{x^2-36=0,} {x ge 5.}}}{}}}}{}$

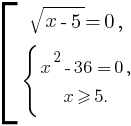
Отсюда:

delim{[}{matrix{3}{1}{{x=5,}{delim{lbrace}{matrix{3}{1}{{delim{[}{matrix{2}{1}{{x=6,}{x=-6,}}}{}} {x ge 5.}}}{}}}}{}

Ответом будут являться числа 5 и 6.