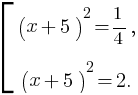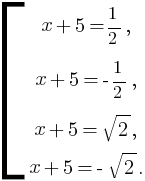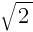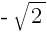Перейти к контенту
Решение уравнений методом замены переменной
Биквадратное уравнение – уравнение вида ax^4 + bx^2 + c = 0, где x – переменная, a, b, c – параметры, но a ≠ 0.
Решают биквадратные уравнения зачастую методом замены переменной (x2 заменяют на другую переменную).
Однородные уравнения второй степени – уравнение, в котором степень всех одночленов, стоящих в левой части уравнения равна двум.
Рассмотрим несколько примеров
Пример 1: Решите уравнение x4 – 2x2 – 3 = 0.
Заменим x2 на переменную t, получим уравнение t2 – 2t – 3 = 0. С помощью дискриминанта находим корни данного уравнения: -1 и 3. Составим совокупность:
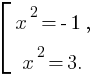
x2 не может быть отрицательным, поэтому не равен -1, получим следующую совокупность:
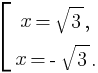
Ответ: 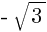 ,
, 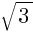 .
.
Пример 2: Решите уравнение 9x – 10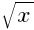 + 1 = 0.
+ 1 = 0.
Примем 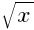 = t, тогда x = t2. Тогда уравнение примет вид: 9t2 – 10t + 1 = 0. С помощью дискриминанта найдём его корни:
= t, тогда x = t2. Тогда уравнение примет вид: 9t2 – 10t + 1 = 0. С помощью дискриминанта найдём его корни: 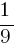 и 1. Составим совокупность:
и 1. Составим совокупность:
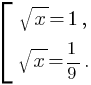
Откуда:
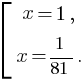
Ответ: 1, 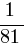 .
.
Пример 3: Решите уравнение 4(x + 5)4 – 9(x + 5)2 + 2 = 0.
Заменим (x + 5)2 на t. Получим уравнение 4t2 – 9t + 2 = 0. Корнями этого уравнения являются числа 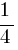 и 2.
и 2.
Составим совокупность:
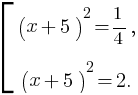
Отсюда:
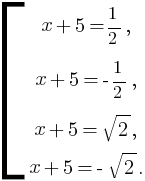
Ответ: -4,5; -5,5; 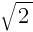 – 5;
– 5; 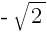 – 5.
– 5.
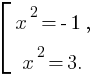
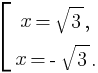
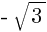 ,
, 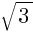 .
.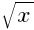 + 1 = 0.
+ 1 = 0.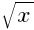 = t, тогда x = t2. Тогда уравнение примет вид: 9t2 – 10t + 1 = 0. С помощью дискриминанта найдём его корни:
= t, тогда x = t2. Тогда уравнение примет вид: 9t2 – 10t + 1 = 0. С помощью дискриминанта найдём его корни: 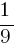 и 1. Составим совокупность:
и 1. Составим совокупность: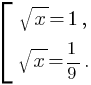
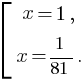
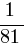 .
.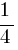 и 2.
и 2.