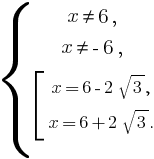Перейти к контенту
Решение уравнений, сводящихся к квадратным уравнениям
Пользуясь теорией, представленной в предыдущей теме, перейдём к решению уравнений:
Рассмотрим несколько примеров
Пример 1: Решите уравнение 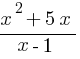 =
= 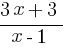 .
.
Найдём область допустимых значений уравнения: x – 1 ≠ 0, откуда x ≠ 1.
Избавимся от знаменателей, домножив обе части на (x – 6), получим 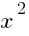 + 2x – 3 = 0. Данное уравнение равносильно системе:
+ 2x – 3 = 0. Данное уравнение равносильно системе:
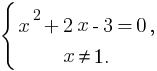
Отсюда:
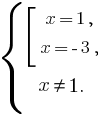
Ответ: -3.
Пример 2: Решите уравнение 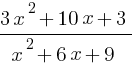 = 0.
= 0.
Разложим на множители поочерёдно числитель и знаменатель, получим 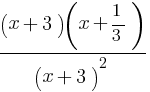 = 0 Сократив на (x + 3), получим
= 0 Сократив на (x + 3), получим 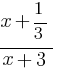 = 0. Данное уравнение равносильно системе:
= 0. Данное уравнение равносильно системе:
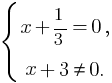
Откуда:
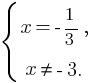
Ответ: 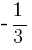 .
.
Пример 3: Решите уравнение 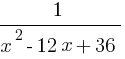 –
– 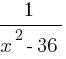 =
= 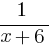 .
.
Приведём все члены уравнения к общему знаменателю, снесём их влево, получим: 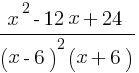 = 0.
= 0.
Найдём через дискриминант корни уравнения 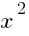 – 12x + 24 = 0: x = 6
– 12x + 24 = 0: x = 6 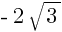 и x = 6 +
и x = 6 +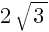 и определим область допустимых значений, получим:
и определим область допустимых значений, получим:
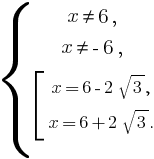
Ответ: 6 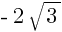 , 6 +
, 6 + 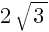 .
.
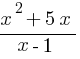 =
= 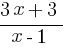 .
.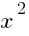 + 2x – 3 = 0. Данное уравнение равносильно системе:
+ 2x – 3 = 0. Данное уравнение равносильно системе: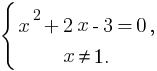
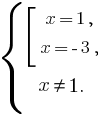
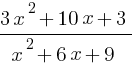 = 0.
= 0.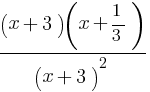 = 0 Сократив на (x + 3), получим
= 0 Сократив на (x + 3), получим 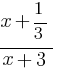 = 0. Данное уравнение равносильно системе:
= 0. Данное уравнение равносильно системе: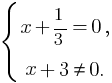
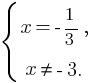
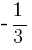 .
.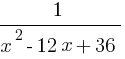 –
– 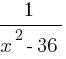 =
= 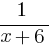 .
.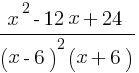 = 0.
= 0.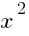 – 12x + 24 = 0: x = 6
– 12x + 24 = 0: x = 6 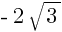 и x = 6 +
и x = 6 +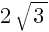 и определим область допустимых значений, получим:
и определим область допустимых значений, получим: