5. Системы уравнений и неравенств как математические модели реальных ситуаций – На 5 !!!

Системы уравнений и неравенств как математические модели реальных ситуаций

Некоторые реальные ситуации можно представить в виде математических моделей, представленных системами уравнений.

Рассмотрим пример математической модели

Пример: Теплоход проходит по реке путь от пункта X в пункт Y за 6 часов, а обратно за 10 часов. За какое время проплывёт плот от пункта X в пункт Y?

Примем за x собственную скорость теплохода, за y – скорость течения реки. Тогда скорость теплохода по течению: x + y, а против течения: x – y. Расстояние между пунктами примем за 1. По имеющимся данным составим систему уравнений:

delim{lbrace}{matrix{2}{1}{{{1}/{x+y}=6,} {{1}/{x-y}=10.}}}{}

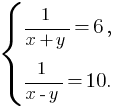
Получим систему:

delim{lbrace}{matrix{2}{1}{{x+y={1}/{6},} {x-y={1}/{10}.}}}{}

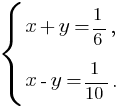
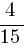Сложим системы, получим 2x = , откуда x = 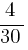= 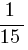км/ч, y = 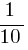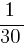– = км/ч, значит плот преодолеет данное расстояние за 30 часов.