Перейти к контенту
Свойства корня n-й степени
Рассмотрим несколько теорем, описывающих свойства корня n-й степени:
1. Для любого a ∈ R и k ∈ N выполняются равенства: 2k + 1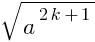 = a и 2k
= a и 2k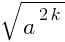 = |a|.
= |a|.
2. Если a ≥ 0 и b ≥ 0, n ∈ N, n > 1, то 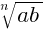 =
= 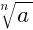
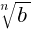 .
.
3. Если a ≥ 0 и b ≥ 0, n ∈ N, n > 1, то 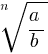 =
= 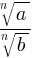 , но если a ≤ 0 и b ≤ 0, n ∈ N, n > 1, то
, но если a ≤ 0 и b ≤ 0, n ∈ N, n > 1, то 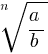 =
= 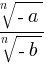 .
.
4. Если a ≥ 0, n ∈ N, k∈ N, n > 1, то 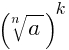 =
= 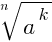 .
.
5. Если a ≥ 0, n ∈ N, k∈ N, n > 1, k > 1, то 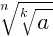 =
= 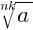 .
.
6. Если a ≥ 0, n ∈ N, k∈ N, n > 1, то 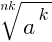 =
= 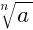 .
.
Рассмотрим несколько примеров
Пример 1: Упростите выражение 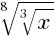 .
.
По теореме (5) получим 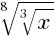 =
= 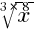 =
= 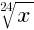 .
.
Пример 2: Внесите множитель под знак корня -5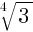 .
.
Возведём 5 в четвёртую степень, внесём под корень: –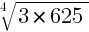 = –
= –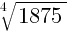 .
.
Пример 3: Сократите дробь 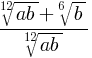 , a > 0, b > 0.
, a > 0, b > 0.
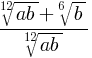 =
= 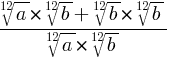 =
= 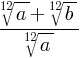 .
.
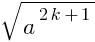 = a и 2k
= a и 2k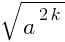 = |a|.
= |a|.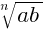 =
= 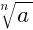
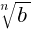 .
.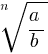 =
= 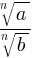 , но если a ≤ 0 и b ≤ 0, n ∈ N, n > 1, то
, но если a ≤ 0 и b ≤ 0, n ∈ N, n > 1, то 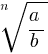 =
= 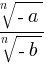 .
.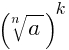 =
= 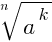 .
.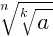 =
= 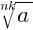 .
.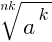 =
= 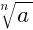 .
.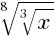 .
.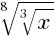 =
= 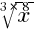 =
= 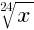 .
.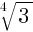 .
.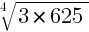 = –
= –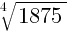 .
.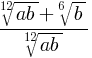 , a > 0, b > 0.
, a > 0, b > 0.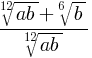 =
= 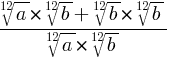 =
= 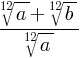 .
.